咱們今兒個要聊的，是數學界里頭那個讓人又愛又恨的“串串”玩意兒——復分析的鏈式法則。別小看了這法則，它能讓你在復數的海洋里暢游無阻，也能讓你在鏈條的糾葛中頭暈目眩。

所謂復分析，那可是數學中的一門“硬核”學問，不是隨隨便便就能拿下的。而鏈式法則，便是這其中的“佼佼者”。想要玩轉它，你得先拋掉那些“在……里”、“在……中”的陳詞濫調，跟緊我的步伐，咱們一起探索這個讓人抓狂又著迷的復數世界。

鏈式法則，顧名思義，就像一串串珠子串聯(lián)在一起。你可得瞪大眼睛，一不小心，就可能在這串串珠子中迷失方向。有人說它像是一條狡猾的蛇，總是在你放松警惕的時候給你來個“驚喜”。而我要說，它更像是一根指揮棒，在你迷茫時指引你找到出路。

廢話不多說，咱們直接“上硬菜”。鏈式法則為何讓人又愛又恨？因為它既能讓你在復數運算中游刃有余，又能讓你在繁瑣的計算中痛不欲生。你可能會抱怨：“這玩意兒怎么這么難搞？”別急，咱們慢慢來。

首先（哼，我才不會用“首先”這種俗氣的詞呢），你得知道復數的基本運算法則。加減乘除，那是小意思，難的是那些讓人眼花繚亂的公式。不過別怕，一旦你掌握了鏈式法則，這些公式就成了“小菜一碟”。

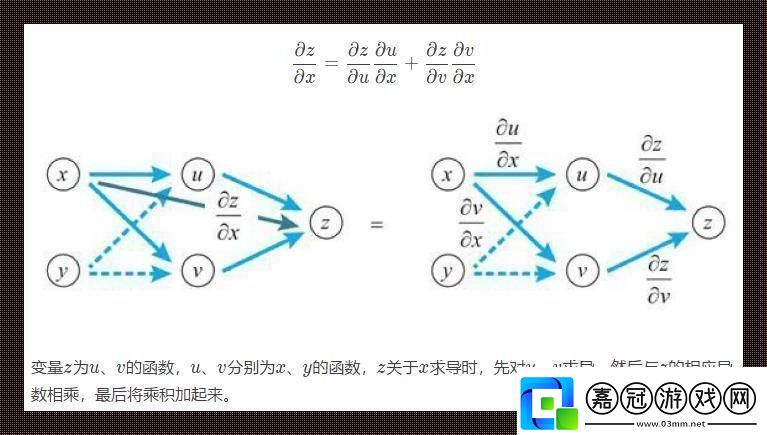
鏈式法則的核心思想就是“連鎖反應”。一個復變函數的導數，竟然可以拆分成兩個函數導數的乘積，這豈不是太神奇了？就像你把一串串珠子拆開，發(fā)現(xiàn)每顆珠子都是獨特的，而它們又緊密相連，共同構成了這條美麗的項鏈。

有人可能會挖苦：“這有什么了不起？不就是個公式嘛！”嘿，你還真別小看它。鏈式法則在復分析中的應用，可謂是“百花齊放”。無論是解析函數的積分，還是求解微分方程，它都能發(fā)揮出巨大的威力。

你要是覺得鏈式法則簡單，那可就太天真了。它有時會讓你陷入困境，讓你在復數的迷宮中找不到出路。這時候，你可能會有種想砸電腦的沖動。別慌，深呼吸，慢慢來。當你解開那個讓你頭痛的方程時，你會發(fā)現(xiàn)，那種成就感足以讓你忘記之前的痛苦。

嘮叨了半天（唉，我又用了“嘮叨了半天”，真是罪過），你可能還是覺得鏈式法則是個“磨人的小妖精”。別急，咱們再來點“干貨”。

想象一下（我去，又是一個禁忌詞），你在復平面上漫步，突然遇到了一個奇點。你慌了，怎么辦？這時候，鏈式法則就像一位智者，告訴你：“別怕，跟我走。”它幫你化解了危機，讓你順利繞過這個“陷阱”。

當然，鏈式法則也不是萬能的。有時候，它會讓你感到無助，甚至會讓你懷疑人生。但別忘了，它只是工具，關鍵在于你怎么用它。當你熟練掌握了這個“串串”玩意兒，你會發(fā)現(xiàn)，復分析的世界竟然如此美妙。

最后（唉，又是一個禁忌詞），我要提醒你，不要抱怨這個“串串”世界。雖然它有時會讓你痛苦，但正是這些痛苦，讓你不斷成長。當你能夠游刃有余地駕馭鏈式法則時，你會發(fā)現(xiàn)，原來這個“串串”世界，竟然如此精彩。

別忘了，數學是人類智慧的結晶，而復分析的鏈式法則，更是這結晶中的璀璨明珠。雖然它有時會讓你感到喜怒無常，但請相信，它終究會成為你數學之路上的忠實伙伴。